残枚数と枚数差無しからのお手つきの影響比較
最終更新日:2015/10/25
執筆者:華郷(@ka_kyo)
1.はじめに
競技かるたにおいて札の増減は取りの成立だけでなく、お手つきによっても発生する。札の取りは1枚差がつくのに対してお手つきは2枚差がつく。そのためお手つきが試合勝敗を分けるターニングポイントになることも少なくない。特に終盤のお手つきは残枚数に対して1枚の重みが強く、勝負の分け目になる。しかしながら、攻めかるたにおいて序盤のお手つきで枚数差が出来、相手陣が出なくなり攻められず負けてしまうという事例があるのも事実である。そこで、本稿ではセイム(持ち札の枚数が自分・相手共に同じ枚数であること)の状態でお手つきした場合に、その後の出札の偏りを考慮した枚数差と枚数推移を期待値で評価した。
2.出札の偏りを考慮した枚数遷移期待値の定式化
相手陣が読まれた時の取得確率をX×100%、自陣が読まれた時の取得確率をY×100%とする。
お手つき時の全枚数をm(m=2k k=1,2,3,4…25)とする。
お手つき後の枚数は式(1-1,2)で表すことが出来る。
自陣の枚数:$a_0=\frac{m+2}{2}$
(1-1)
相手陣の枚数:$b_0=\frac{m-2}{2}$
(1-2)
式(1-1,2)より、1枚読まれたときの期待値は式(2-1,2)となる。
相手陣が読まれる確率:$p_b (0)=\frac{b_0}{m-0}=\frac{m-2}{2m}$
(2-1)
自陣が読まれる確率:$p_a (0)=\frac{a_0}{m-0}=\frac{m+2}{2m}$
(2-2)
上記式より、自陣の札の減少期待値は式(3-1,2)で表される。
出札が相手陣:
$⊿a_{b0}=p_b (0)×X=\frac{X(m-2)}{2m}$
(3-1)
出札が自陣:
$⊿a_{a0}=p_a (0)×Y=\frac{Y(m+2)}{2m}$
(3-2)
また、相手陣の札の減少期待値は式(4-1,2)で表すことができる。
出札が相手陣:
$⊿b_{b0}=p_b(0)×(1-X)=\frac{(1-X)(m-2)}{2m}$
(4-1)
出札が自陣:
$⊿b_{a0}=p_a(0)×Y=\frac{(1-Y)(m+2)}{2m}$
(4-2)
式(1)~式(4)より、自陣、相手陣のそれぞれの枚数は次の式(5-1,2)であらわされる。
自陣の枚数:
$a_1=a_0-⊿a_{b0}-⊿a_{a0}$
$=a_0-p_b (0)×X-p_a (0)×Y$
$=a_0-\frac{b_0×X}{m-0}-\frac{a_0×Y}{m-0}$
$=a_0×\frac{m-0-Y}{m-0}-b_0×\frac{X}{m-0}$
(5-1)
相手陣の枚数:
$b_1=b_0-⊿b_{b0}-⊿b_{a0}=$
$b_0-p_b (0)×(1-X)-p_a(0)×(1-Y)$
$=b_0-\frac{b_0×(1-X)}{m-0}-\frac{a_0×(1-Y)}{m-0}$
$=a_0×\frac{(Y-1)(m-0)}+b_0×\frac{m-0-(1-X)}{m-0}$
(5-2)
式(5)より枚数遷移は連立漸化式で表されることが分かる。導出が割愛するが、出札枚数をnとして式(6-1,2)の連立漸化式が導ける。(まだちゃんと導出はしていないです。)
自陣の枚数:
$a_{n+1}=a_n×\frac{m-n-Y}{m-n}-b_n×\frac{X}{m-n} ,$
$a_0=\frac{m+2}{2}$
(6-1)
相手陣の枚数:
$b_{n+1}=a_n×\frac{Y-1}{m-n}-b_n×\frac{m-n+1-X}{m-n} ,$
$b_0=\frac{m-2}{2}$
(6-2)
ここで、式(6-1,2)から一般項を出すのもよいがこのまま数値計算することにする。
3.実際の遷移の検討
EXCELを用いて式(1-1,2)(6-1,2)を計算する。X=1、Y=0、つまり相手陣が出ると100%抜けるが、自陣が出ると100%相手に取られるとする。その時の枚数差と枚数比率(自陣の残枚数/相手陣の残枚数)を評価する。枚数比率は低いほど負けていることになり、0となったとき負けとなる。たとえば25枚セイムだと1となり、自陣20枚-相手陣10枚だと0.5となり、相手陣0枚で0となる。その時の枚数差のグラフを図1に枚数比率のグラフを図2に示す。
まず、お手つき時(セイムの状態でお手つきした時点)のグラフ(実線)に注目する。図1の枚数差はどの時点でも2枚であるが、図2の枚数比率は試合が進むごとに差が大きくなる。これは1枚の重みが試合が進むにつれて大きくなることを示す。残16枚(8枚セイム)を切った当たりから急激に枚数比率の変化が大きくなりこれ以降のお手つきはその時点で大きな影響を与えるということが分かる。これは序盤のお手つきは実力差があれば挽回可能であるが、終盤のお手つきは実力差があっても挽回することが難しいことが分かる。
次に出札の偏りを考慮したグラフ(破線)に注目する。図1の枚数差の枚数が増えなくなっている部分と図2の比率が0を下回っている部分はその時点で相手陣が0となり試合が終了したことを示す。どちらのグラフでも実力差が無く相手陣を抜きあう場合、序盤のお手つきの方が終盤の時点で響いてくることが分かる。
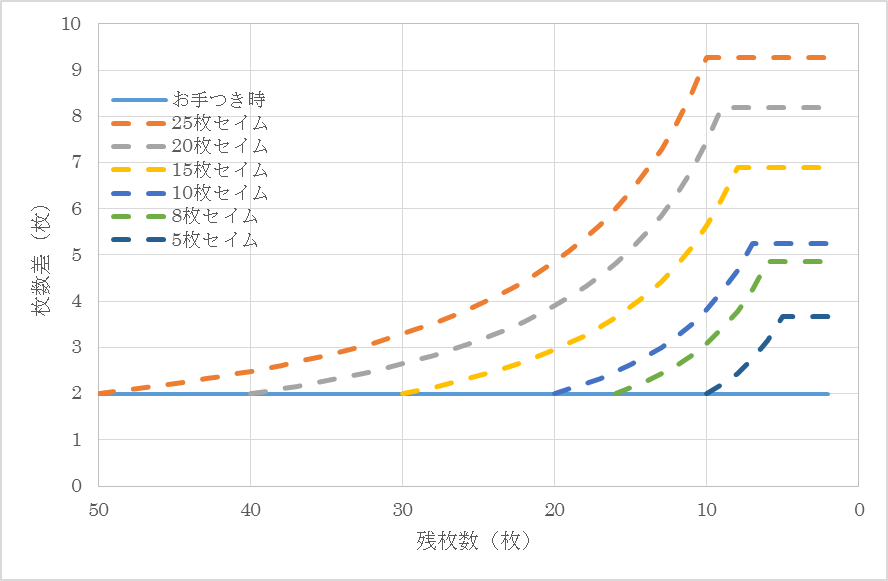
図1 残枚数別の枚数差比較(相手陣取得確率100%自陣取得確率0%)
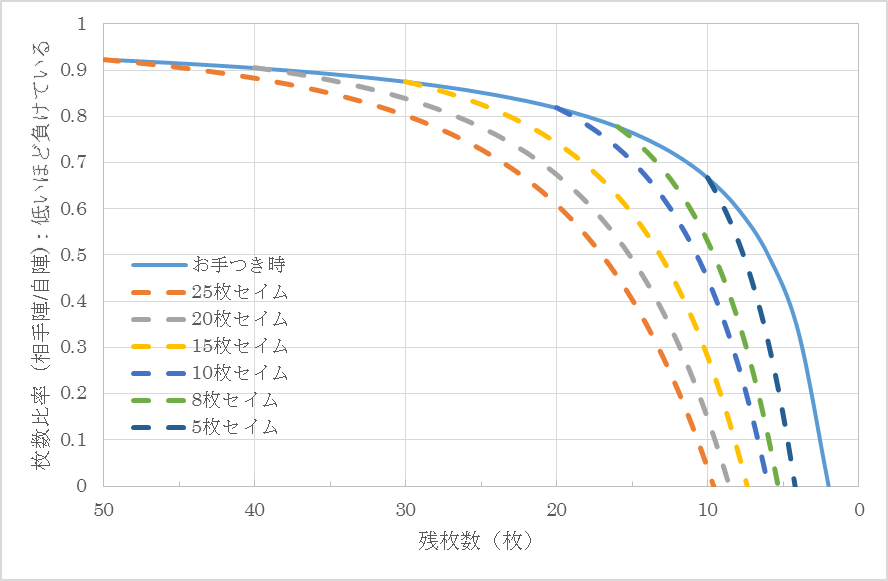
図2 残枚数別の枚数比率比較(相手陣取得確率100%自陣取得確率0%)
図3に相手陣取得確率80%自陣取得確率20%の場合の枚数遷移を示す。図2と比較すると自陣の取得確率を上げると実力差は無い場合でも序盤のお手つきの影響は小さくなることが分かる。
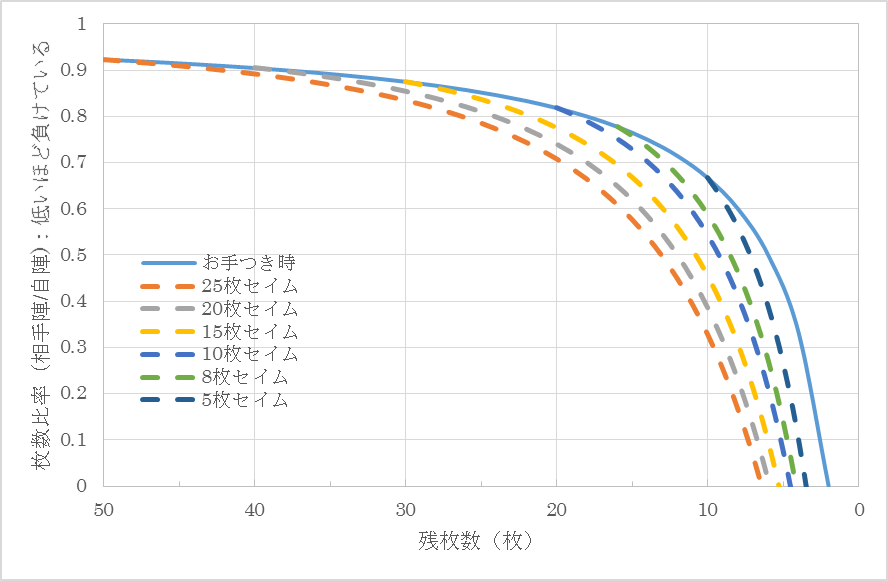
図3 残枚数別の枚数比率比較(相手陣取得確率80%自陣取得確率20%)
図4に実力差が少しある場合で自分の方が強い場合の結果を示す。相手陣取得確率80%自陣取得確率30%とする。序盤のお手つきは攻め主体でも挽回できるが枚数が減るにつれて挽回が難しくなることが分かる。
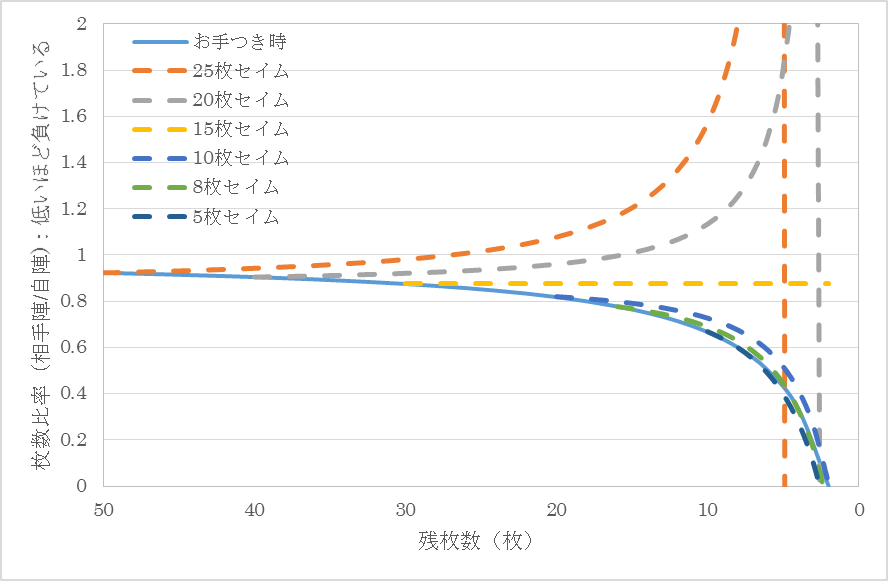
図4 残枚数別の枚数比率比較(相手陣取得確率80%自陣取得確率30%)
4.最後に
本稿ではセイム時のお手つきについて、残枚数とお手つきの影響について検討した。また、序盤のお手つきによる出札の偏りを考慮した枚数遷移を検討した。実力が互角同士の場合差は大きくなり、相手陣取得比率が高いほど差が開きやすいことを示した。また、実力差がある場合も後半になるにつれて挽回が難しくなることを示した。
一方、今回の検討は期待値によるモデルの一例であり、序盤でお手付きをしても確率的に2連取して追いつく場合もある。追いつくとその時点で互角となる。つまりばらつきが考慮されていないのである。何%でどの程度の差が開くか、などの検討はする必要があると考えられる。
初稿:2015/10/25